Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 혼공머신러닝딥러닝
- Brightics Studio
- 영상제작기
- 브라이틱스 서포터즈
- 포스코 아카데미
- 혼공머신
- 데이터분석
- Brigthics를 이용한 분석
- 직원 이직률
- 노코드AI
- 삼성SDS
- 직원 이직여부
- 개인 의료비 예측
- 삼성SDS Brightics
- Brightics
- 데이터 분석
- 혼공학습단
- 브라이틱스
- 캐글
- 삼성SDS Brigthics
- 삼성 SDS Brigthics
- 추천시스템
- 포스코 청년
- Brightics를 이용한 분석
- 모델링
- Brigthics
- 삼성 SDS
- 팀 분석
- 혼공
- Brigthics Studio
Archives
- Today
- Total
데이터사이언스 기록기📚
[추천시스템] 기초 선형 수학 본문
📌목차
[행렬 연산 예시]
1. 내적과 Element-wise 연산
2. 전치 행렬
3. 역행렬
4. 대각행렬
5. 고유값과 고유 벡터
6. 랭크
7. SVD
[유사도 메트릭]
1. 코사인 유사도와 유클리드 거리 비교
📌행렬 연산 예시
1. 내적과 Element-wise 연산
- 내적(dot product) : 두 벡터의 각 자리 원소의 곱 → 모두 더한 값
- 원소별 연산(Element-wise) : 두 행렬 or 벡터의 각 원소끼리 곱하는 것
- 내적(np.dot())
a = np.array([1,2,3])
b = np.array([4,5,6])
# 내적 과정
print("\n", a[0]*b[0], "+", a[1]*b[1], "+", a[2]*b[2])
print("Dot product of a and b:", np.dot(a,b))
# 내적
print(np.dot(a,b))
# 출력 값
# 4 + 10 + 18
# Dot product of a and b: 32
# 32
- 원소별 연산(a*b)
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print( a * b) # 그냥 곱하기만 함
# 출력값
#[ 4 10 18]
- 행렬 곱셈 (np.matmul)
import numpy as np
# Define two 2x2 matrices
A = np.array([[1, 2],
[3, 4]])
B = np.array([[5, 6],
[7, 8]])
# Calculate the result matrix by matrix multiplication
C = np.matmul(A, B) # 행렬 곱셈
# Show the calculation of each element in the result matrix
print("Matrix A:")
print(A)
print("\nMatrix B:")
print(B)
print("\nC[0, 0] = A[0, 0] * B[0, 0] + A[0, 1] * B[1, 0] = (1 * 5) + (2 * 7) =", 1*5 + 2*7)
print("C[0, 1] = A[0, 0] * B[0, 1] + A[0, 1] * B[1, 1] = (1 * 6) + (2 * 8) =", 1*6 + 2*8)
print("C[1, 0] = A[1, 0] * B[0, 0] + A[1, 1] * B[1, 0] = (3 * 5) + (4 * 7) =", 3*5 + 4*7)
print("C[1, 1] = A[1, 0] * B[0, 1] + A[1, 1] * B[1, 1] = (3 * 6) + (4 * 8) =", 3*6 + 4*8)
print("\nResult Matrix C:")
print(C)
2. 전치 행렬
- 행렬 전치(transpose) : 행과 열을 바꿈.
- 추천 알고리즘 사용 예) MF, ALS
a = np.array([[1,2,3],
[4,5,6]])
a_transpose = np.transpose(a)
print('원래 a 행렬\n', a)
print('\n전치 후 a 행렬\n', a_transpose)
print('\n전치 후 a 행렬\n', a.T)
3. 역행렬
- 역행렬(linalg.inv)
- 원 행렬 * 역행렬 = 단위행렬
- 사용되는 곳 : 연립 방정식의 해 구할 때, SVD 계산 시 사용
A = np.array([[2, 3],
[4, 5]])
A_inverse = np.linalg.inv(A)
print('역행렬\n', A_inverse)
print('\nA * A역행렬\n', np.matmul(A,A_inverse))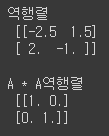
4. 대각행렬
- 대각행렬(diag) : 대각선 외의 모든 요소가 0
- 계산 단순화 하는데 이용
A = np.diag([1,1,1])
print('대각행렬\n', A)
5. 고유값과 고유 벡터
6. 랭크
- 랭크(linalg.matrix_rank) : 행렬에서 독립적인 열 or 행 벡터의 최대 개수
- 열 or 행 벡터에 사칙연산 해도 해당 값이 나오지 않을 때, 최대의 개수
[기초 선형대수] 행렬에서 Rank (랭크) 란?
선형대수에서 등장하는 Rank 라는 개념에 대해서 간략하게 알아보자. 위키의 정의를 우선 확인해보...
blog.naver.com
A = np.array([[9,8,7],
[6,5,4],
[3,2,1]])
rank_A = np.linalg.matrix_rank(A)
print('원래 A\n', A)
print('\nrank A\n',rank_A)
728x90
'추천시스템' 카테고리의 다른 글
| [추천시스템] 컨텐츠 기반 필터링(Content-Based Filtering) (0) | 2024.03.28 |
|---|---|
| [추천시스템] 고전적인 추천 알고리즘 (0) | 2024.03.06 |
| [추천시스템] 기본 추천시스템 - Best Seller 추천/사용자 집단별 추천 (0) | 2023.08.04 |
| [추천시스템] 주요 추천시스템 알고리즘 (0) | 2023.08.01 |
Comments




