| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 직원 이직률
- Brightics Studio
- 삼성SDS
- 브라이틱스
- 삼성 SDS Brigthics
- 혼공학습단
- 삼성SDS Brigthics
- 삼성 SDS
- Brightics
- Brigthics
- 삼성SDS Brightics
- 혼공머신러닝딥러닝
- 혼공머신
- 캐글
- 영상제작기
- 개인 의료비 예측
- 혼공
- 모델링
- 포스코 아카데미
- 데이터분석
- 데이터 분석
- 직원 이직여부
- 브라이틱스 서포터즈
- 포스코 청년
- Brigthics를 이용한 분석
- Brigthics Studio
- Brightics를 이용한 분석
- 팀 분석
- 노코드AI
- 추천시스템
- Today
- Total
데이터사이언스 기록기📚
[이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.8 다이나믹 프로그래밍 본문
[이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.8 다이나믹 프로그래밍
syunze 2022. 4. 29. 22:081. 다이나믹 프로그래밍
중복되는 연산을 줄이자
- 컴퓨터를 활용해도 해결하기 어려운 문제
- 최적의 해를 구하기에 시간이 매우 많이 필요 (연산 속도의 한계)
- 메모리 공간이 매우 많이 필요한 문제 (메모리 공간을 사용할 수 있는 데이터 개수 한정)
→ 연산 속도와 메모리 공간을 최대한 활용할 수 있는 효율적인 알고리즘을 작성
- 다이나믹 프로그래밍 / 동적 계획법(Dynamic Programming)
- 메모리 공간을 약간 더 사용하면 연산 속도를 비약적으로 증가시킬 수 있는 방법
- 예시) 피보나치 수열 : 이전 두 항의 합을 현재의 항으로 설정하는 특징이 있는 수열
- 점화식 - 인접한 항들 사이의 관계식, 점화식으로 수열의 항이 이어지는 형태 간결하게 표현.
- 프로그래밍에서 피보나치 수열을 배열, 리스트로 표현할 수 있다.
(수열 - 여러 개의 수가 규칙에 따라서 배열된 형태를 의미)


# 피보나치 함수 소스코드
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x - 1) + fibo(x - 2)
print(fibo(4))- 문제
- 동일한 함수 반복적으로 호출 → 불필요한 계산 많아짐
- f(n) 함수에서 n이 커지면 커질 수록, 수행 시간 기하급수적 증가 → 시간 복잡도 O(2**n)

- 해결책
- 다이나믹 프로그램 사용하여 해결
- 다이나믹 프로그램 조건
1) 큰 문제 → 작은 문제로 나눌 수 있다.
2) 작은 문제 구현한 정답 → 그것을 포함하는 큰 문제에서도 동일
- 메모이제이션(캐싱: 값을 저장하는 방법) 기법
- 다이나믹 프로그래밍 구현하는 방법 중 한 종류
- 한 번 구한 결과를 메모리 공간에 메모, 같은 식을 호출하면 메모한 결과를 그대로 가져오는 기법
- 구현 : 한 번 구한 정보를 리스트에 저장 → 같은 정보 필요 시 구한 정답 리스트에서 가져오기
- 성능 : 반복문 > 재귀 함수
- 시간 복잡도 : O(N)
- 구현 방법
1) [메모이제이션] 탑다운 방식 - 하향식 (큰 문제 해결 → 작은 문제 호출)
# 피보나치 수열 소스코드(재귀적)
# 한 번 계산된 결과를 메모이제이션 하기 위한 리스트 초기화
d = [0] * 100
# 피보나치 함수를 재귀함수로 구현(탑다운 다이나믹 프로그래밍)
def fibo(x):
# 종료 조건(1 or 2일때 1을 반환)
if x == 1 or x == 2:
return 1
# 이미 계산한 적 있는 문제라면 그대로 반환
if d[x] != 0:
return d[x]
# 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
d[x] = fibo(x - 1) + fibo(x - 2)
return d[x]
print(fibo(99))2) [전형적인 형식] 보텀업 방식 - 상향식 (반복문 이용하여 소스코드 작성, 작은 문제부터 차근차근 답 도출)
- DP테이블 : 보텀업 방식에서 사용되는 결과 저장용 리스트
# 피보나치 수열 소스코드(반복적)
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 100
# 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1
d[2] = 1
n = 99
# 피보나치 함수 반복문으로 구현(보텀업 다이나믹 프로그래밍)
for i in range(3, n + 1):
d[i] = d[i - 1] + d[i - 2]
print(d[n])다이나믹 프로그래밍
- 큰 문제를 작게 나눔
- 같은 문제, 한 번씩만 풀어 문제를 효율적으로 해결하는 알고리즘 기법
+) 분할정복 알고리즘(퀵 정렬) : 정렬할 리스트 분할, 전체적으로 정렬이 될 수 있도록 함. (자리 잡으면 값 변경X)
+) 다이나믹 프로그램 : 문제들이 서로 영향을 미침(한 번 해결한 문제를 다시금 해결 - 답 저장)
- 추가적인 개념
- 메모이제이션은 사전 자료형(수열처럼 연속적이지 않은 경우 유용) 이용할 수 있다
- 문제 푸는 방법
- 완전 탐색 시 오래걸림, 부분 문제의 중복 여부 확인 → 문제가 다이나믹 프로그래밍 유형임을 파악
- 재귀함수 작성 후 → 메모이제이션 효율적이면 코드 개선
- 탑다운 방식 << 보텀업 방식으로 구현하는 것 권장
- 재귀의 깊이가 깊어서 나는 오류 - sys.setrecursionlimit() 함수 호출하여 재귀 완화
📌2. 1로 만들기
✔️문제
정수 X가 주어질 때, 정수 X에 사용할 수 있는 연산은 다음과 같이 4가지이다.
- X가 5로 나누어떨어지면, 5로 나눈다.
- X가 3으로 나누어떨어지면, 3으로 나눈다.
- X가 2로 나누어떨어지면, 2로 나눈다.
- X에서 1을 뺀다.
연산 4개를 이용하여 1을 만드려고 함
✔️입력 조건
첫째 줄에 정수 X가 주어진다. (1 <= X <= 30,000)
✔️출력 조건
첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.
✔️입력 예시
26
✔️출력 예시
3
✔️나의 문제 풀이
- (큰 수부터) 5,3,2로 나누기 -> 1) 나눠지는 경우, 통과 2) 1빼고 나누기
- 답 도출 실패
x = int(input())
first_x = x
d = []
cnt = 0
# (큰 수부터)2,3,5로 나누기 -> 1) 나눠지는 경우, 통과 2) 1빼고 나누기
def div(x):
if x % 5 == 0:
x /= 5
d.append(x)
ans(x)
elif x % 3 == 0:
x /= 3
d.append(x)
ans(x)
elif x % 2 == 0:
x /= 2
d.append(x)
ans(x)
def remain(x):
x -= 1
d.append(x)
ans(x)
div(x)
def ans(x):
if x == 1.0:
return len(d)
remain(x)
print(len(d))
print(d)
✔️책의 문제 풀이
- 예시) X = 6
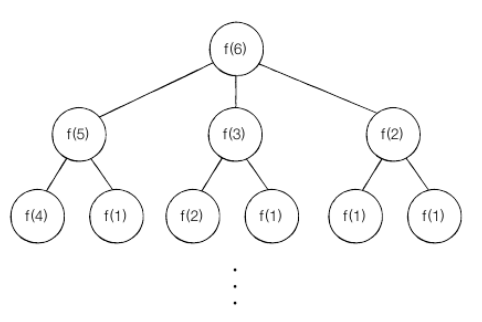
- 점화식
# 정수 x를 입력받기
x = int(input())
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 30001
# 다이나믹 프로그래밍 진행(보텀업)
for i in range(2, x + 1):
# 현재의 수에서 1을 빼는 경우
d[i] = d[i - 1] + 1
# 현재의 수가 2로 나누어 떨어지는 경우
if i % 2 == 0:
d[i] = min(d[i], d[i // 2] + 1)
# 현재의 수가 3으로 나누어 떨어지는 경우
if i % 3 == 0:
d[i] = min(d[i], d[i // 3] + 1)
# 현재의 수가 5로 나누어 떨어지는 경우
if i % 5 == 0:
d[i] = min(d[i], d[i // 5] + 1)
print(d[x])
✔️책의 문제 풀이와 나의 문제풀이 비교
- DP 테이블 설정 안함
- 각 점화식 마다 1을 더하는 이유는 각 연산이 한 번씩 실행되었기 때문
📌3. 개미 전사
✔️문제
메뚜기 마을의 식량창고 일직선으로 이어져 있다.
각 식량창고에서 정해진 수의 식량을 저장, 개미 전사는 식량창고 선택적으로 약탈하여 식량을 빼앗을 예정.
메뚜기 정찰병들은 일직선상에 존재하는 식량창고 중 식량창고가 공격 받으면 바로 알아챌 수 있다.
개미 전사가 정찰병에게 들키디 않고 식량창고를 약탈하기 위해서는 최소한 한 칸 이상 떨어진 식량창고를 약탈해야한다.
개미 전사를 위해 식량창고 N개에 대한 정보가 주어졌을 때, 얻을 수 있는 식량의 최댓값을 구하는 프로그램 작성하기.
✔️입력 조건
- 첫째 줄에 식량창고의 개수 N이 주어진다. (3 <= N <= 100)
- 둘째 줄에 공백으로 구분되어 각 식량창고에 저장된 식량의 개수 K가 주어진다. (0 <= K <= 1,000)
✔️출력 조건
첫째 줄에 개미 전사가 얻을 수 있는 식량의 최댓값을 출력하시오.
✔️입력 예시
4
1 3 1 5
✔️출력 예시
8
✔️나의 문제풀이
- 입력예시와 출력예시를 만족하긴 했지만, DP 테이블 이용 안하고 출력
- 마지막 원소가 답이 아닐 수도 있다는 생각을 함
n = int(input())
food = list(map(int,input().split()))
for i in range(3, n):
food[i] = max(food[i-2], food[i-3]) + food[i]
print(food.pop())- 바로 앞의 값을 제외하고, 계속 더해가며 max값 찾기(계속 더하면 max는 i-2, i-3에서 고를 수 있기 때문)
n = int(input())
save = list(map(int,input().split()))
dp =[0] * n
dp[0], dp[1] = save[0], save[1]
for i in range(2,n):
dp[i] = max(save[:i-1]) + save[i]
print(max(dp))
✔️책의 문제풀이
- 문제를 그림으로 도식화 : 식량을 선택할 수 있는 경우

- 왼쪽부터 차례대로 식량창고 턴다고 가정, 점화식 세우기
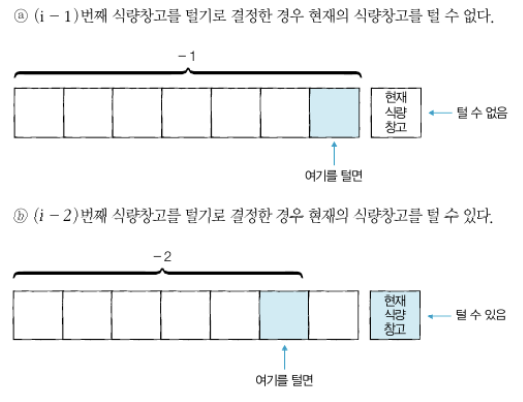
- 점화식
- 왼쪽부터 (i-3)번째 이하의 식량창고는 고려할 필요 X → 한 칸 이상 떨어진 식량창고는 항상 털 수 있음
# 정수 N을 입력받기
n = int(input())
# 모든 식량 정보 입력잗기
array = list(map(int, input().split()))
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 100
# 다이나믹 프로그래밍 진행(보텀업)
d[0] = array[0]
d[1] = max(array[0], array[1])
for i in range(2, n):
d[i] = max(d[i-1], d[i-2]+array[i])
# 계산된 결과 출력
print(d[n-1])
✔️나의 문제풀이와 책의 문제풀이 비교
- 이 문제는 굳이 DP 테이블을 만들 필요가 있는가..?하는 문제. 그냥 받은 리스트에서 업데이트 하는 방식은 안되는건가? → DP 테이블 없이 진행하면 리스트 값이 업데이트 되어서 나중에 헷갈릴 수 있음. DP 테이블 만들기.
- 책에서는 직전 식량과 2번째 전 식량 + 현재식량 비교, 나는 2번째 3번째 비교 + 현재식량 비교.
→ 나의 문제풀이는 직전 식량이 최대일 경우 오류가 날 가능성 있음
- 그래도 이전 식과 연관을 지어서 생각한건 굿
📌4. 바닥 공사
✔️문제
가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 얇은 바닥이 있다.
이 얇은 바닥을 1 *2의 덮개, 2 * 1의 덮개, 2 * 2의 덮개를 이용해 채우고자 한다.
이때 바닥을 채우는 모든 경우의 수 구하기
✔️입력 조건
첫째 줄에 N이 주어진다. (1 <= N <= 1,000)
✔️출력 조건
첫째 줄에 2 * N크기의 바닥을 채우는 방법의 수를 796,796으로 나눈 나머지를 출력한다.
✔️입력 예시
3
✔️출력 예시
5
✔️나의 문제풀이
- 짝수, 홀수 나누어서 경우의 수 생각
- n을 1과 2의 합으로 나누어야한다는 아이디어 생각
- n이 2로 이루어지는 조합일 때 2가지 경우의 수가 있다는 것도 생각
- 마지막 답은 '같은 것이 있는 순열'로 나와야 함 → 점화식으로 풀려고 노력
- 끼워 맞추기로 예시만 맞음
n = int(input())
d = [0] * 796796
# 1로 다 쪼개지면 경우의 수는 1개 -> 전체 개수에서 +1
# 2로 쪼개지는 경우면 2*1, 2*2 -> 그림이 달라질 수 있는 경우 추가
# '같은 것으로 이루어진 순열' 풀기위한 팩토리얼 식
def factorial(x):
if x <= 1:
return 1
return x * factorial(x - 1)
# 짝수, 홀수 나눠서 생각
if n % 2 == 0:
m = n // 2
else:
m = (n-1) // 2
# 같은 것으로 이루어진 순열
for j in range(m,0,-1):
d[j] = 1
d[j-1] = factorial((j-1) + (2*1)) / factorial(j-1) * factorial(2)
print(sum(d))
✔️책의 문제풀이
- 왼쪽부터 차례대로 덮개로 채운다고 생각하기
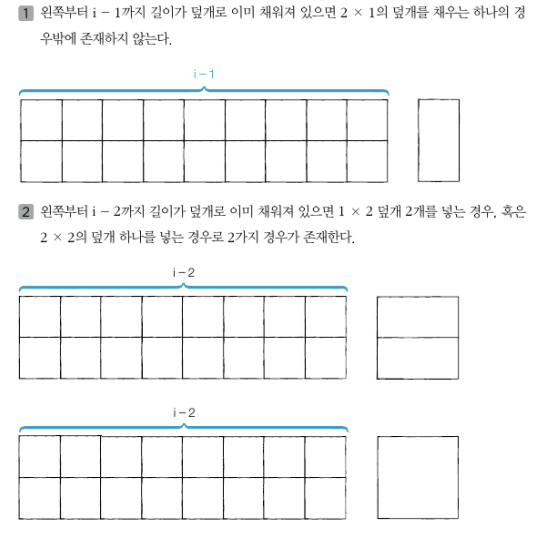
- (N - 2) 미만의 길이에 대해서는 고려할 필요 없음
- 점화식
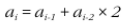
# 정수 n을 입력받기
n = int(input())
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 1001
# 다이나믹 프로그래밍 진핸(보텀업)
d[1] = 1
d[2] = 3
for i in range(3, n + 1):
d[i] = (d[i - 1] + 2 * d[i - 2]) % 796796 # 결과값이 굉장히 커질 수 있어서 나누는 것
# 계산된 결과 출력
print(d[n])
✔️나의 문제풀이와 책의 문제풀이 비교
- 아이디어 나쁘지 않았음. 조금만 더 점화식이랑 연결시키기.
- 짝수, 홀수 나눔 → 점화식이랑 연결시키기
📌5. 효율적인 화폐 구성
✔️문제
N가지 종류의 화폐가 있다. 이 화폐들의 개수를 최소한으로 이용해서 그 가치의 합이 M원이 되도록 하려한다.
이때 각 화폐는 몇 개라도 사용할 수 있으며, 사용한 화폐의 구성은 같지만 순서만 다른 것은 같은 경우로 구분.
✔️입력 조건
- 첫째 줄에 N,M이 주어진다. (1 <= N <= 100, 1 <= M <= 10,000)
- 이후 N개의 줄에는 각 화폐의 가치가 주어진다. 화폐 가치는 10,000보다 작거나 같은 자연수이다.
✔️출력 조건
- 첫째 줄에 M원을 만들기 위한 최소한의 화폐 개수를 출력한다.
- 불가능할 때는 -1을 출력한다.
✔️입력 예시
2 15
2
3
✔️출력 예시
5
✔️나의 문제풀이
- 완성 못함
# n - 화폐 종류, m - m원
n, m = map(int, input().split())
# DP 테이블 초기화
d = [0] * 100001
# 화폐의 가치
money = []
for _ in range(n):
money.append(int(input()))
for j in range(2,m):
for i in range(len(money)):
if m - money[i] >= 0:
d[1] = 1
d[j] =
if m == d[m]:
print('-1')
else:
print(d[m])
✔️책의 문제풀이
- 점화식 (최소한의 화폐 개수 : ai, 화폐의 단위 : k)

- N = 3, M = 7이고 각 화폐의 단위가 2, 3, 5인 경우
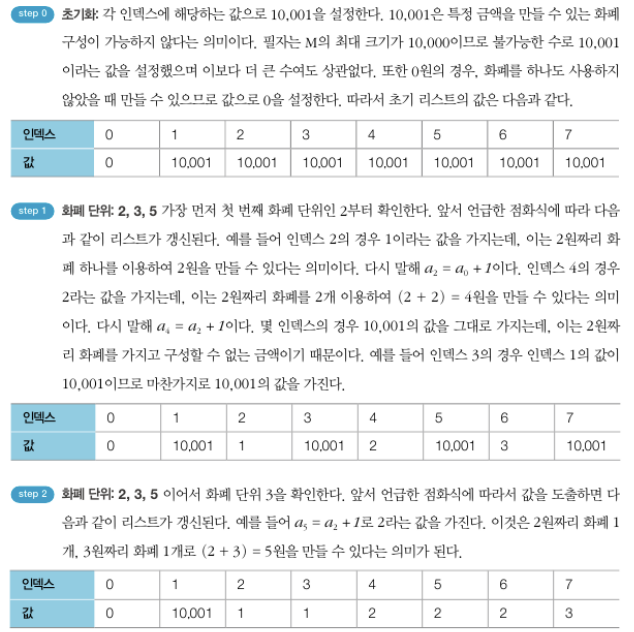
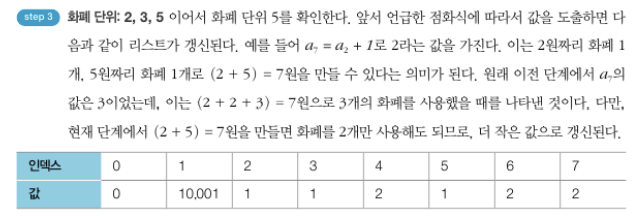
- 소스코드
# 정수 n,m을 입력받기
n, m = map(int, input().split())
# N개의 화폐 단위 정보를 입력받기
array = []
for i in range(n):
array.append(int(input()))
# 한 번 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [10001] * (m+1)
# 다이나믹 프로그래밍 진행(보텀업)
d[0] = 0
for i in range(n):
for j in range(array[i], m+1):
if d[j - array[i]] != 10001: # (i - k)원을 만드는 방법이 존재하는 경우
d[j] = min(d[j], d[j - array[i]] + 1)
# 계산된 결과 출력
if d[m] == 10001: # 최종적으로 M원을 만드는 방법이 없는 경우
print(-1)
else:
print(d[m])
✔️나의 문제풀이와 책의 문제풀이 비교
- 하나씩 더하는 방식을 어떻게 점화식으로 풀어내는지 이해하지 못했으나 답지보고 이해 완료
'Coding Test > 이것이 취업을 위한 코딩테스트이다 with 파이썬' 카테고리의 다른 글
| [이것이 취업을 위한 코딩테스트이다 with 파이썬] Ch.14 정렬 문제 (0) | 2023.03.02 |
|---|---|
| [이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.9 최단 경로 (0) | 2022.04.29 |
| [이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.7 이진 탐색 (0) | 2022.04.22 |
| [이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.6 정렬 (0) | 2022.04.19 |
| [이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.4 구현 (0) | 2022.04.14 |




