| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 추천시스템
- 영상제작기
- 삼성SDS Brightics
- 포스코 아카데미
- 삼성 SDS Brigthics
- 혼공머신
- 직원 이직률
- 개인 의료비 예측
- 포스코 청년
- Brigthics를 이용한 분석
- Brigthics
- 캐글
- Brightics
- 팀 분석
- 삼성SDS Brigthics
- 혼공학습단
- 혼공머신러닝딥러닝
- 데이터분석
- Brightics Studio
- 브라이틱스
- 혼공
- 직원 이직여부
- 브라이틱스 서포터즈
- 노코드AI
- 데이터 분석
- Brigthics Studio
- 삼성 SDS
- 삼성SDS
- 모델링
- Brightics를 이용한 분석
- Today
- Total
데이터사이언스 기록기📚
[삼성 SDS Brightics 서포터즈] #07_팀 프로젝트_개인 의료비 예측(2) 본문
안녕하세요~!
두 번째 팀 프로젝트로 돌아온 Brightics 서포터즈입니다!
이전 포스팅에서는 데이터 분석 목적과 EDA 부분에 초점을 맞춰 포스팅을 진행하였습니다.
이전 포스팅이 궁금하시다면 아래 링크를 클릭해주세요!
[삼성 SDS Brightics 서포터즈] #06_팀 프로젝트_개인 의료비 예측(1)
안녕하세요~! 오랜만에 돌아온 Brightics 서포터즈입니다! 이번 포스팅부터 약 7주간 팀 프로젝트를 진행하게 됩니다! 저희 팀의 프로젝트 궁금하지 않으신가요?!?! 이번 포스팅의 목차는 다음과 같
subinze.tistory.com
이전 포스팅에서는 전체를 다 다룬 포스팅이었다면,
이번 포스팅부터는 팀원들과 역할을 나누어 진행하기로 하였습니다!
역할은
1. 변수 간의 상관관계를 Spearman, Pearson 이용하여 분석
2. 통계 검정
3. 이상치, 결측치, 중복 값 처리
4. 데이터 분할 및 기본 모델 사용
5. 데이터 기본 모델 파라미터 조정
로 나누어 진행하였는데요.
저는
통계 검정 부분을 맡아 진행하기로 하였습니다!
목차는 다음과 같습니다.

그럼 팀 프로젝트 두 번째 포스팅 시작하겠습니다!
1. 카이제곱 분석 - 독립성 검정
먼저 두 범주형 변수의 관계를 알아보기 위해
카이제곱 검정 중 독립성 검정을 실시하였습니다!
카이제곱 검정에서는 통계적 가설이 있는데요,
귀무가설(H0) : 범주형 변수가 서로 독립적이다.
대립가설(H1) : 범주형 변수가 서로 의존적이다.
의 가설을 기준으로 분석을 진행합니다.
귀무가설(H0)인지 대립가설(H1)인지 판단하는 여부는
p-value를 기준으로 판단하게 됩니다.
p-value란 유의 확률로
귀무가설(H0)이 참이라는 가정 하에 표본 데이터가 귀무가설을 지지하는 확률을 의미합니다!
유의 수준(α)이 0.05일 때,
유의 확률(p-value)이 유의 수준(α) 보다 작으면 대립가설(H1)을 채택하고
유의확률(p-value)이 유의수준(α)보다 크면 귀무가설(H0)을 채택하게 됩니다!
Brightics Studio에서는 2개 이상의 범주형 변수간 독립성 검정을 위해
Chi-square Test of Independence
블록을 제공하고 있습니다!
해당 블록을 이용하여
데이터에서 범주형 변수인
sex, smoker, region에 대해 독립성 검정을 진행해 보았습니다!
1-1. Smoker
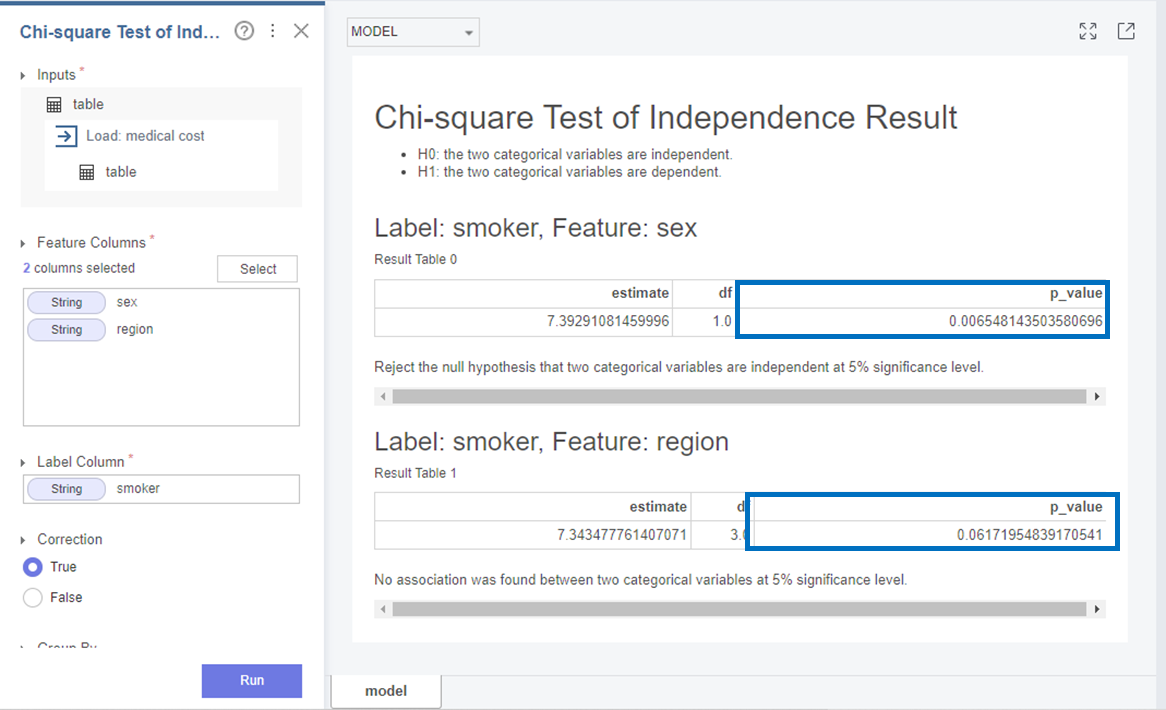
먼저 sex와 smoker는
p-value가 0.0065로 0.05보다 작아 귀무가설(H0)을 기각하고 대립가설(H1)을 채택합니다.
즉, sex와 smoker 변수는 독립적이 아니고 연관이 있다는 것을 알 수 있었습니다!
다음으로 region와 smoker는
p-value가 0.061로 0.05보다 커 귀무가설(H0)을 채택합니다.
즉, region과 smoker 변수는 독립적이며 연관이 없다는 것을 알 수 있었습니다!
1-2. sex
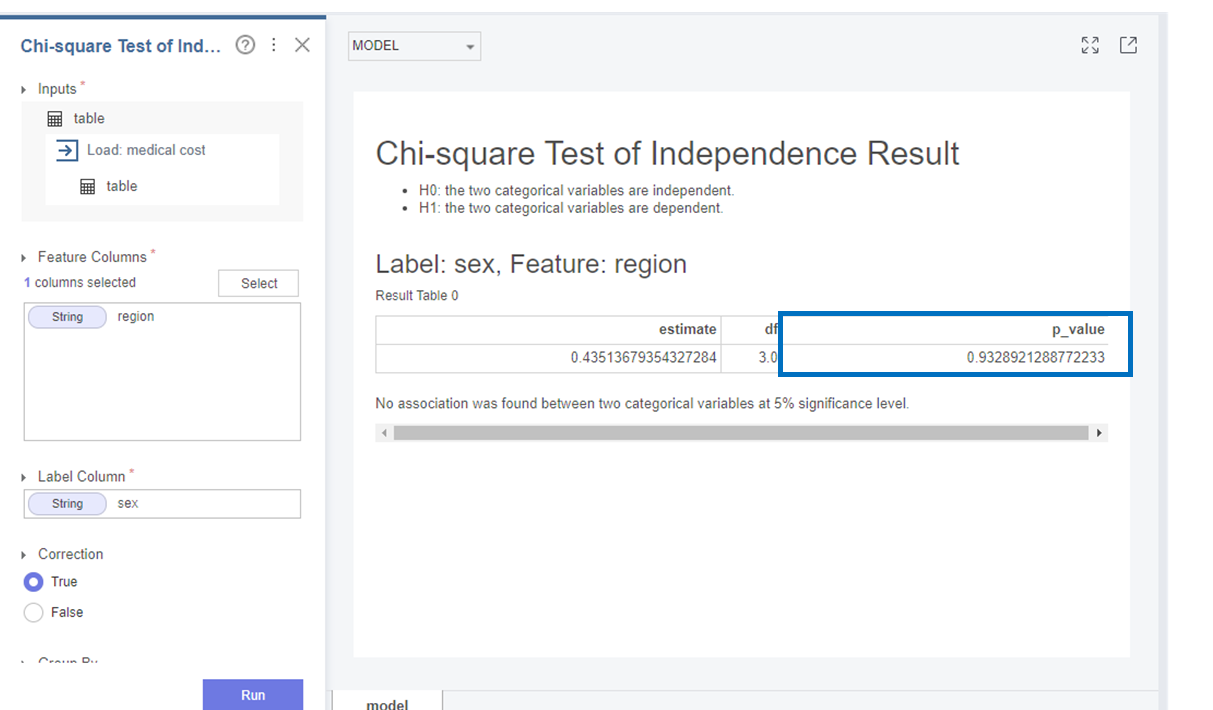
다음으로 region과 sex는
p-value가 0.932로 0.05보다 커 귀무가설(H0)를 채택합니다.
즉, region과 sex변수는 독립적이며 연관이 없다는 것을 알 수 있었습니다!
2. Kruskal-Wallis Test
집단 간 평균 및 분산 차이를 알아보기 위해서는
정규성 검정 확인 후 진행하여야 합니다!
변수별 정규성 검정을 확인한 후 검정을 진행해보겠습니다.
2-1. 정규성 검정
정규성 검정은
Brigthics Studio에서 제공하는 Normality Test를 이용하여 진행하였습니다!
정규성 검정에서는
귀무가설(H0) : 표본 분포는 정규분포를 따른다.
대립가설(H1) : 표본 분포는 정규분포를 따르지 않는다.
의 가설을 가지고 판단하게 됩니다.
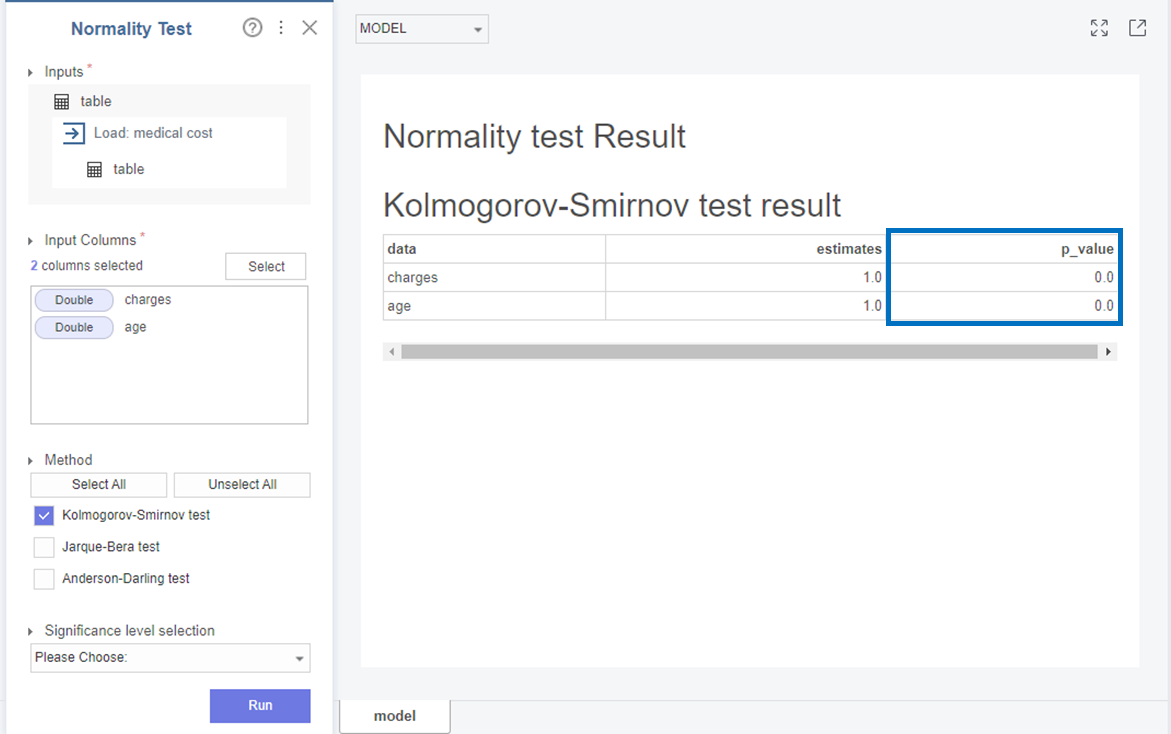
먼저 Charges와 age는
p-value가 0으로 0.05보다 작아 귀무가설(H0)을 기각하고 대립가설(H1)을 채택합니다.
즉, Charges와 age 변수는 표본 분포는 정규분포를 따르지 않습니다!
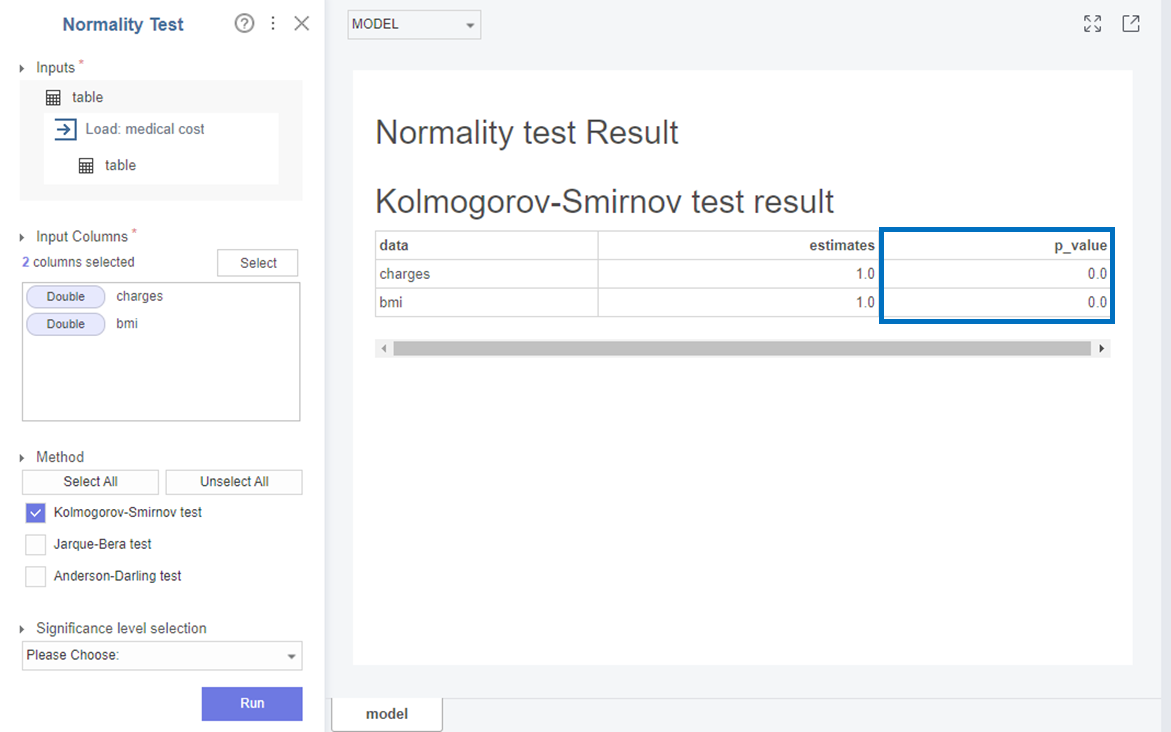
다음으로 Charges와 bmi는
p-value가 0으로 0.05보다 작아 귀무가설(H0)을 기각하고 대립가설(H1)을 채택합니다.
즉, Charges와 bmi 변수는 표본 분포는 정규분포를 따르지 않습니다!

다음으로 Charges와 children은
p-value가 0으로 0.05보다 작아 귀무가설(H0)을 기각하고 대립가설(H1)을 채택합니다.
즉, Charges와 children변수는 표본 분포는 정규분포를 따르지 않습니다!
수치형 변수 모두 정규분포를 따르지 않는 것을 확인할 수 있었습니다!
2-2. Kruskal-Wallis Test
수치형 변수 모두 정규분포를 만족하지 않아
Kruskal-Wallis Test를 이용하여 분포 확인을 진행하였습니다!
분포 확인은
Brigthics Studio에서 제공하는 Kruskal-Wallis Test를 이용하여 진행하였습니다!
Kruskal-Wallis Test에서는
귀무가설(H0) : 모든 그룹의 크기(또는 분포)가 같다.
대립가설(H1) : 모든 그룹의 크기(또는 분포)는 다르다.
의 가설을 가지고 판단하게 됩니다.
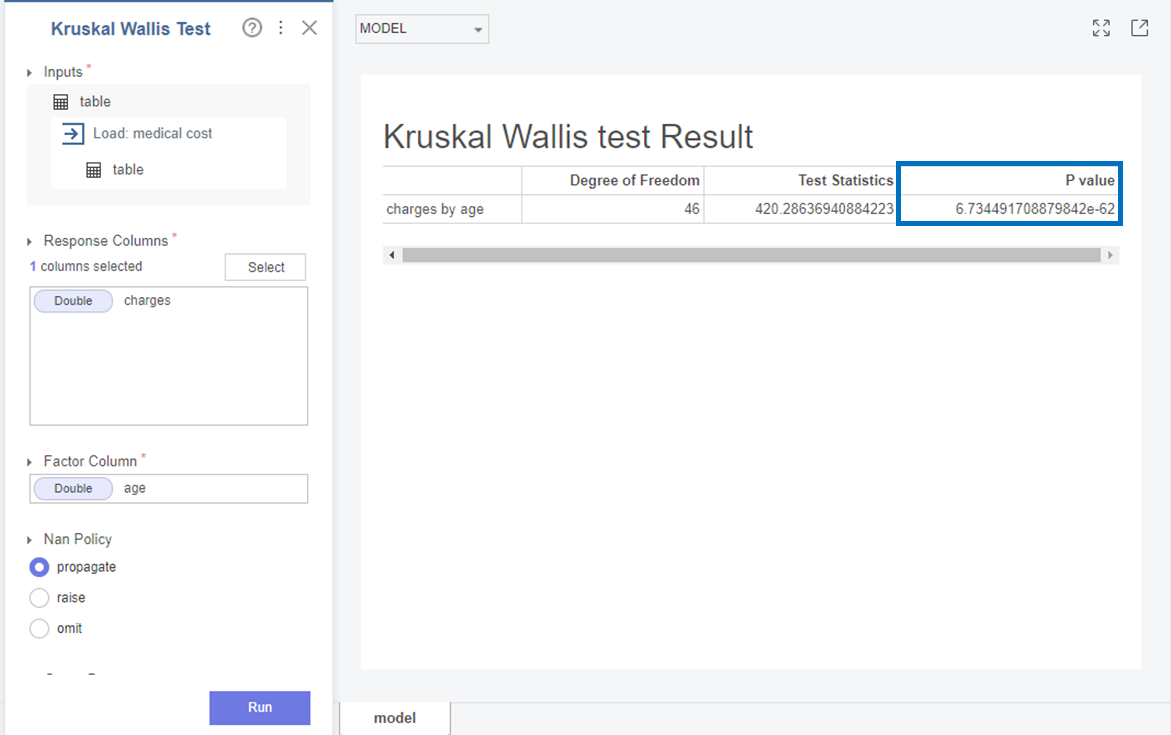

먼저 Charges와 age는
p-value가 6.73e-62로 0.05보다 작아 귀무가설(H0)을 기각하고 대립가설(H1)을 채택합니다.
즉, Charges와 age 변수의 분포는 다르다는 것을 확인할 수 있었습니다!
다음으로 Charges와 sex는
p-value가 0.728로 0.05보다 커 귀무가설(H0)을 채택합니다.
즉, Charges와 sex 변수의 분포는 같다는 것을 확인할 수 있었습니다!
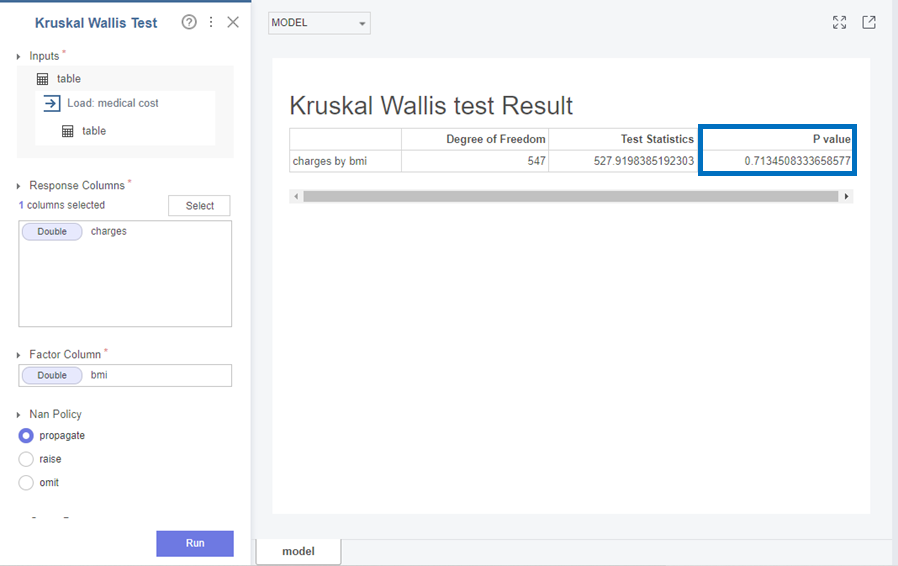
다음으로 Charges와 bmi는
p-value가 0.713으로 0.05보다 커 귀무가설(H0)을 채택합니다.
즉, Charges와 bmi 변수의 분포는 같다는 것을 확인할 수 있었습니다!
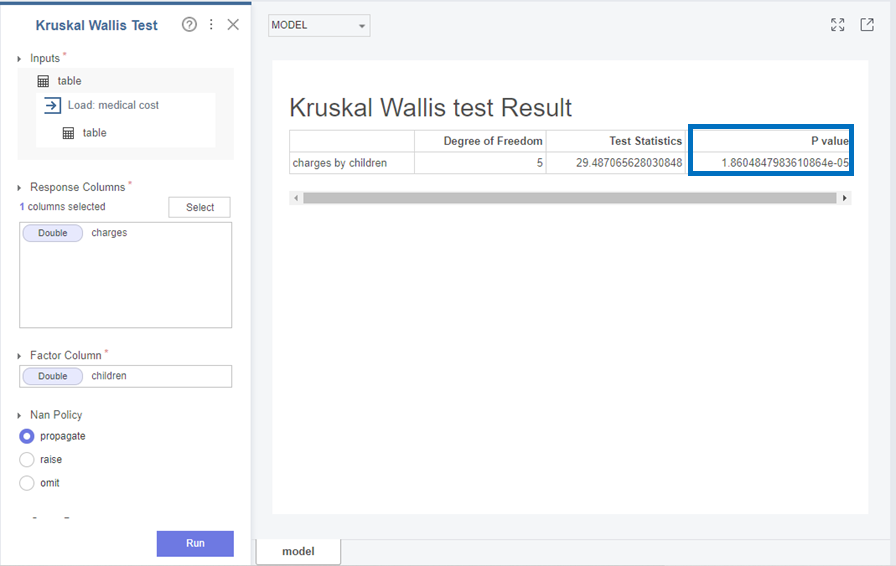
다음으로 Charges와 children은
p-value가 1.86e-05으로 0.05보다 작아 귀무가설(H0)을 기각하고 대립가설(H1)을 채택합니다.
즉, Charges와 children변수의 분포는 다르다는 것을 확인할 수 있었습니다!
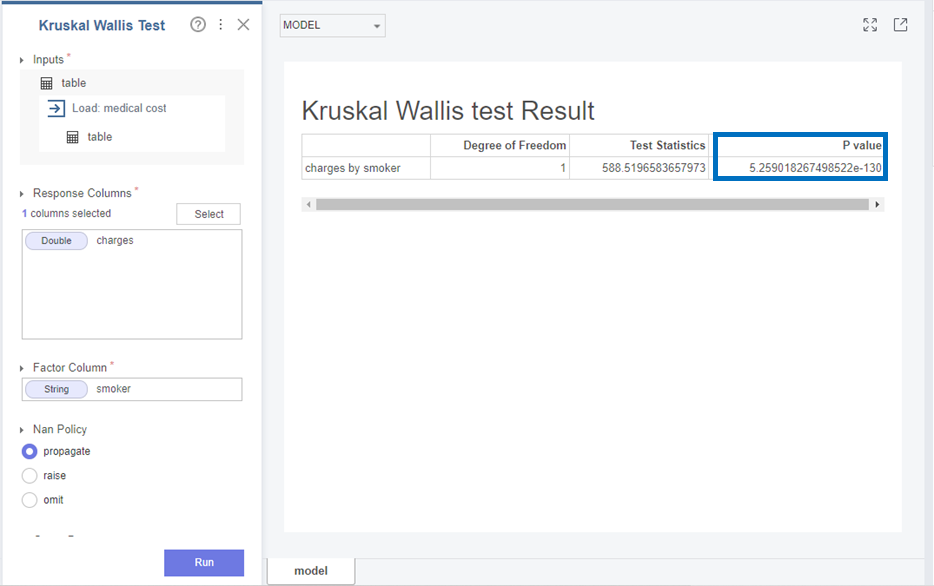
다음으로 Charges와 smoker는
p-value가 5.25e-130으로 0.05보다 작아 귀무가설(H0)을 기각하고 대립가설(H1)을 채택합니다.
즉, Charges와 smoker변수의 분포는 다르다는 것을 확인할 수 있었습니다!
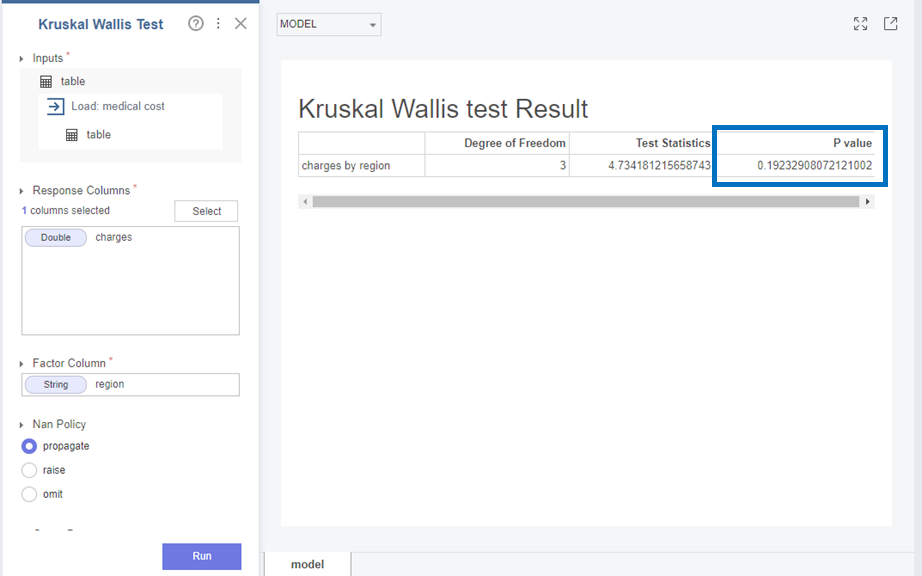
다음으로 Charges와 region은
p-value가 0.19로 0.05보다 커 귀무가설(H0)을 채택합니다.
즉, Charges와 region변수의 분포는 같다는 것을 확인할 수 있었습니다!
오늘 포스팅을 통해
변수의 의존성과 분포에 대해서 알아보았는데요,
분석을 진행할 때 EDA로만 판단하고 넘어가는 경향이 있었는데
통계적 검정으로 데이터의 분포를 정확히 확인해 볼 수 있어서
통계적 검정의 필요성을 다시 한번 더 느낄 수 있었습니다!
또한 통계적 검정을 진행해보면서
통계적 검정의 지식 또한 얻을 수 있어 뜻깊었습니다!
팀원들과 진행하는 팀 프로젝트 2주 차를 지나가고 있는데
열정적인 팀원들과 꼼꼼한 팀원들 덕분에 팀 프로젝트가 잘 진행되고 있는 거 같아 매우 든든합니다ㅎㅎ
다음 포스팅은
모델링 부분으로 다시 찾아오겠습니다!
* 본 포스팅은 삼성 SDS Brightics 서포터즈 3기 활동의 일환으로 작성하였습니다 *
'대외활동 > 삼성SDS Brightics 서포터즈' 카테고리의 다른 글
| [삼성 SDS Brightics 서포터즈] #09_팀 프로젝트_개인 의료비 예측(4) (1) | 2022.09.06 |
|---|---|
| [삼성 SDS Brightics 서포터즈] #08_팀 프로젝트_개인 의료비 예측(3) (0) | 2022.08.30 |
| [삼성 SDS Brightics 서포터즈] #06_팀 프로젝트_개인 의료비 예측(1) (0) | 2022.08.16 |
| [삼성 SDS Brightics 서포터즈] #05_개인 프로젝트(1) 고객 성격 분석_데이터 전처리(2), 모델링, 분석 (0) | 2022.07.12 |
| [삼성 SDS Brightics 서포터즈] #04_개인 프로젝트(1) 고객 성격분석_데이터 전처리 (0) | 2022.07.05 |



