| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 혼공머신
- 직원 이직여부
- 삼성SDS
- Brightics를 이용한 분석
- Brightics
- 브라이틱스 서포터즈
- Brigthics
- 모델링
- 포스코 청년
- 개인 의료비 예측
- 데이터 분석
- 삼성SDS Brightics
- 삼성 SDS
- Brightics Studio
- 삼성SDS Brigthics
- 브라이틱스
- 포스코 아카데미
- 팀 분석
- 데이터분석
- 혼공
- Brigthics Studio
- Brigthics를 이용한 분석
- 추천시스템
- 노코드AI
- 직원 이직률
- 캐글
- 삼성 SDS Brigthics
- 영상제작기
- 혼공머신러닝딥러닝
- 혼공학습단
- Today
- Total
데이터사이언스 기록기📚
[이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.5 DFS/BFS 본문
[이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.5 DFS/BFS
syunze 2023. 3. 7. 21:241. 꼭 필요한 자료구조 기초
- 탐색(search) : 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정
- (프로그래밍) 그래프, 트리 안에서 탐색하는 문제
- 대표적으로 BFS/DFS(사전학습 : 스택, 큐, 재귀 함수)
- 자료구조(Data Structure) : 데이터를 표현하고 관리, 처리하기 위한 구조
[핵심적인 함수]
1) 삽입(Push) : 데이터를 삽입한다.
2) 삭제(Pop) : 데이터를 삭제한다.
[추가 고민]
+) 오버플로 : 특정한 자료구조가 수용할 수 있는 데이터 크기 이미 가득 찬 상태에서 삽입 연산 수행할 때 발생
(저장 공간 벗어나 데이터 넘처흐를 때 발생)
+) 언더플로 : 특정한 자료구조에 데이터가 전혀 들어 있지 않은 상태에서 삭제 연산 수행할 때 발생
(데이터 전혀 없는 상태에서 발생)
🎈스택
- 스택(Stack)

- (쌓을 때) 아래 → 위
- (뺄 때) 위 → 아래 형태
- 선입후출. 후입선출 구조.
- 예시
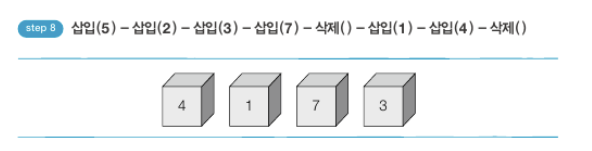
# 스택 예제
stack =[]
# 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
stack.append(5)
stack.append(2)
stack.append(3)
stack.append(7)
stack.pop()
stack.append(1)
stack.append(4)
stack.pop()
print(stack) # 최하단 원소부터 출력
print(stack[::-1]) # 최상단 원소부터 출력
- 파이썬에서 스택 사용 (별도의 라이브러리 X)
- list.append() : 리스트 가장 뒤쪽에 데이터 삽입
- list.pop() : 리스트 가장 뒤쪽에 데이터 꺼냄
🎈큐
- 큐(Queue) : 공정한 자료구조

- 먼저 온 사람이 먼저 들어가고, 먼저 나온다.
- 선입선출 구조
- 예제


# 큐 예제
from collections import deque
# 큐 구현을 위해 deque 라이브러리 사용
queue = deque()
# 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
queue.append(5)
queue.append(2)
queue.append(3)
queue.append(7)
queue.popleft() # 왼쪽부터 쌓이고 왼쪽부터 빠져서 popleft 사용
queue.append(1)
queue.append(4)
queue.popleft()
print(queue) # 먼저 들어온 순서대로 출력
queue.reverse() # 다음 출력을 위해 역순으로 바꾸기
print(queue) # 나중에 들어온 원소부터 출력
- 파이썬에서 큐 사용
- collections 모듈에서 제공하는 deque 자료구조 이용
(deque : 스택과 큐의 장점을 모두 채택, 데이터 넣고 빼는 속도가 리스트 자료형보다 효율적. queue 라이브러리 이용하는 것보다 더 간단)- deque.append() : 리스트 삽입
- deque.popleft() : 리스트 맨 앞 삭
- deque → list 변경 : list(queue) 이용
🎈재귀함수
- 재귀함수(Recursive Function) : 자기자신을 다시 호출하는 함수
- 프랙털 구조와 흡사(ex. 삼각형 안에 또 다른 삼각형이 무한히 존재하는 그림)
# 재귀함수 예제
# 실행시 계속 값 출력
def recursive_function():
print('재귀 함수를 호출합니다.')
recursive_function()
recursive_function()
- 재귀함수의 종료 조건
- 종료조건 명시하지 않으면 함수 무한 호출 될 수 있음
- 재귀함수 수행 : 스택 이용(마지막에 호출한 함수가 먼저 수행을 끝내야 그 앞의 함수 호출이 종료)
- 스택 이용하는 상당수 알고리즘은 '재귀함수' 사용 (ex. DFS)
# 재귀 함수 종료 예제
def recursive_function(i):
# 100번째 출력했을 때 종료되도록 종료 조건 명시
if i == 100:
return
print(i, '번째 재귀 함수에서', i+1,'번째 재귀 함수를 호출합니다.')
recursive_function(i+1)
print(i,'번째 재귀 함수를 종료합니다.')
recursive_function(1)
- 팩토리얼 예제
- 반복적으로 구현한 방식
# 반복적으로 구현한 n!
def factorial_iterative(n):
result = 1
# 1부터 n까지의 수를 차례대로 곱하기
for i in range(1,n+1):
result *= i
return result
print('반복적으로 구현:',factorial_iterative(5))
# 출력) 반복적으로 구현 : 120- 재귀적으로 구현한 방식
- 재귀함수의 코드가 더 간결
- 점화식을 소스코드로 옮김
(점화식 - 특정한 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것을 의미) - 재귀 함수 내에 특정 조건일 때, 함수를 호출하지 않고 종료하도록 if문 작성
# 재귀적으로 구현한 n!
def factorial_recursive(n):
if n <= 1: # n이 1 이하인 경우 1를 반환
return 1
# n! = n * (n-1)!를 그대로 코드로 작성하기
return n * factorial_recursive(n-1)
print('재귀적으로 구현:', factorial_recursive(5))
# 출력) 재귀적으로 구현: 1202. 탐색 알고리즘 DFS/BFS
🎈DFS
- DFS(Depth-First Search)
- 깊이 우선 탐색. 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
- 그래프 기본 구조

- 그래프 : 노드(정점), 간선으로 구성
- 두 노드가 간선으로 연결 = 두 노드는 인접하다
- 그래프 표현 방식
1) 인접 행렬(Adjacency Matrix) : 2차원 배열로 그래프의 연결관계 표현
- 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식
(행,열 : 노드 번호 / 표 값 : 거리) - 2차원 리스트로 구현 가능
- 연결되어 있지 않는 노드 - 무한의 비용(999999999으로 선언)

# 인접 행렬 방식 예제
INF = 999999999 # 무한의 비용 선언
# 2차원 리스트를 이용해 인접 행렬 표현
graph = [
[0,7,5],
[7,0,INF],
[5,INF,0]
]
print(graph)
2) 인접 리스트(Adjacency List) : 리스트로 그래프의 연결 관계를 표현하는 방식
- 연결리스트 이용
- 파이썬 : 2차원 리스트 (노드, 거리)로 저장
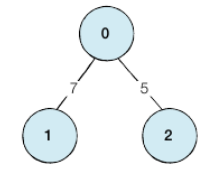

# 인접 리스트 방식 예제
# 행이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]
# 노드 0에 연결된 노드 정보 저장(노드, 거리)
graph[0].append((1,7))
graph[0].append((2,5))
# 노드 1에 연결된 노드 정보 저장(노드, 거리)
graph[1].append((0,7))
# 노드 2에 연결된 노드 정보 저장(노드, 거리)
graph[2].append((0,5))
print(graph)
# 출력 : [[(1, 7), (2, 5)], [(0, 7)], [(0, 5)]]
- 그래프 표현 방식 비교
- 메모리 측면 : 인접행렬(모든 관계 저장) → 노드 개수 많을 수록 메모리 불필요하게 낭비
인접리스트(연결된 정보만 저장) → 메모리 효율적으로 사용 - 속도 측면 : 인접행렬(모든 관계 저장) → 찾는거 빠름
인접리스트(연결된 정보만 저장) → 속도가 느림(연결된 데이터 하나씩 확인)
→ 특정한 노드와 연결된 인접노드 순회 : 인접 행렬 - 찾기쉬움 / 인접 리스트 - 메모리 공간 낭비 적음
- DFS 특징 및 구체적인 동작 과정
- DFS는 스택 자료구조 이용(재귀함수 이용시 간결하게 구현 가능)
- 시간 복잡도 : (탐색 수행할 때 데이터 개수가 N개인 경우) O(N)
- 동작 과정 :
1) 탐색 시작 노드 - 스택에 삽입, 방문 처리함
(방문처리 : 처리된 노드가 다시 삽입되지 않게 체크하는 것, 각 노드를 한 번씩만 처리할 수 있음)
2) 스택의 최상단 노드에 방문하지 않은 인접 노드 있음 → 인접 노드 스택에 삽입, 방문처리
방문하지 않은 인접 노드 없음 → (스택) 최상단 노드 꺼냄
3) 2)과정을 더 이상 수행할 수 없을 때까지 반복
+ 인접한 노드 중 방문하지 않는 노드 여러개 - 번호가 낮은 순서부터 처리
- DFS 예제






# DFS 예제
def dfs(graph, v, visited):
# 현재 노드를 방문 처리
visited[v] = True
print(v, end = ' ')
# 현재 노드와 연결된 다른 노드를 재귀적으로 방문 -> 깊게 탐색 가능
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [
[], # 노드 1부터 시작해서 인덱스 0인 부분 비워둠
[2,3,8], # 1번 노드부터 인접한 노드 작성
[1,7], # 2번 노드
[1,4,5], # 3번 노드
[3,5],
[3,4],
[7],
[2,6,8],
[1,7] # 8번 노드
]
# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9 # 인덱스 0은 사용하지 않도록 초기화
# 정의된 DFS 함수 호출
dfs(graph, 1, visited)
# 출력 : 1 2 7 6 8 3 4 5→ DFS는 스택, 재귀함수 사용
그림에서 위로 나오는 것(스택에서 노드 꺼내는 것) - 재귀함수 종료 의미
🎈BFS
- BFS(Breadth First Search)
- 너비 우선 탐색 알고리즘. 가까운 노드부터 탐색하는 알고리즘.
- BFS 구현 및 동작 방식
- 구현 - 큐(파이썬 : deque 사용)
- 동작방식
1) 탐색 시작 노드 - 큐 삽입, 방문처리 함
2) 큐에서 해당 노드 꺼냄 - 해당 노드의 인접 노드 중 방문하지 않는 노드를 큐에 삽입 후 방문처리
3) 2)의 과정을 더 이상 수행할 수 없을 때까지 반복
- BFS 예제





# BFS 예제
from collections import deque
# BFS 메서드 정의
def bfs(graph, start, visited):
# 큐 구현 위해 deque 라이브러리 사용
queue = deque([start])
# 현재 노드를 방문 처리
visited[start] = True
# 큐가 빌 때까지 반복
while queue:
# 큐에서 하나의 원소를 뽑아 출력
v = queue.popleft()
print(v, end = ' ')
# 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [
[],
[2, 3, 8],
[1, 7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9
# 정의된 BFS 함수 호출
bfs(graph, 1, visited)+) BFS - 큐 자료구조 이용. deque 라이브러리 사용.
+) 시간 복잡도 O(N)→ DFS보다 수행 시간 좋음
🎈DFS와 BFS의 비교
| DFS | BFS | |
| 동작 원리 | 스택 | 큐 |
| 구현 방법 | 재귀함수 이용 | 큐 자료구조 이용 |
- 문제 팁
- 1차원, 2차원 배열 → 그래프 형태로 생각
📌3. 음료수 얼려 먹기
✔️문제
N * M 크기의 얼음 틀이 있다.
구멍이 뚫려 있는 부분은 0, 칸막이가 존재하는 부분은 1로 표시된다.
구멍이 뚫려 있는 부분끼리 상, 하, 좌, 우로 붙어 있는 경우 서로 연결되어 있는 것으로 간주한다.
얼음 틀의 모양이 주어졌을 때, 생성되는 총 아이스크림의 개수 구하기.
✔️입력 조건
- 첫 번째 줄에 얼음 틀의 세로 길이 N과 가로 길이 M이 주어진다.(1 <= N,M <= 1,000)
- 두 번째 줄부터 N+1번째 줄까지 얼음 틀의 형태가 주어진다.
- 이때 구멍이 뚫려있는 부분은 0, 그렇지 않은 부분은 1이다.
✔️출력 조건
한 번에 만들 수 있는 아이스크림의 개수를 출력한다.
✔️입력 예시

✔️출력 예시
8
✔️나의 풀이
- DFS 무한 반복문에서 빠져나오지 못
n,m = map(int,input().split())
li = []
visit = []
ans = 0
for _ in range(n):
li.append(list(map(int,input())))
def dfs(li,x,y):
visit.append((x,y))
# 정지해주기 위한 조건
if x < 0 or x >= len(li[0]) or y < 0 or y >= len(li):
return -1
if li[x+1][y] == 0:
return dfs(li,x+1,y)
elif li[x][y+1] == 0:
return dfs(li,x,y+1)
elif li[x-1][y] == 0:
return dfs(li,x-1,y)
elif li[x][y-1] == 0:
return dfs(li,x,y-1)
return -1
for x in range(len(li[0])):
for y in range(len(li)):
if (x,y) not in visit and li[x][y] == 0:
dfs(li,x,y)
ans += 1
print(ans)
✔️책의 문제풀이
- 해결방법
- 특정한 지점의 주변 상, 하, 좌, 우를 살펴본 뒤에 주변 지점 중에서 값이 '0'이면서 아직 방문하지 않은 지점이 있다면 해당 지점을 방문한다.
- 방문한 지점에서 다시 상, 하, 좌, 우를 살펴보면서 방문을 다시 진행하면, 연결된 모든 지점을 방문할 수 있다.
- 앞 과정을 모든 노드에 반복하며 방문하지 않은 지점의 수를 센다
# N,M을 공백으로 구분하여 입력받기
n,m = map(int, input().split())
# 2차원 리스트의 맵 정보 입력받기
graph = []
for i in range(n):
graph.append(list(map(int, input())))
# DFS로 특정한 노드를 방문한 뒤에 연결된 모든 노드들도 방문
def dfs(x,y):
# 주어진 범위를 벗어나는 경우에는 즉시 종료
if x <= -1 or x >= n or y <= -1 or y >= m:
return False
# 현재 노드를 아직 방문하지 않았다면
if graph[x][y] == 0:
# 해당 노드 방문 처리
graph[x][y] = 1
# 상, 하 ,좌, 우의 위치도 모두 재귀적으로 호출
dfs(x - 1, y)
dfs(x, y - 1)
dfs(x + 1, y)
dfs(x, y + 1)
return True
return False # 조건 만족하지 못하는 경우(graph[x][y] == 1일때)
# 모든 노드(위치)에 대하여 음료수 채우기
result = 0
for i in range(n):
for j in range(m):
# 현재 위치에서 DFS 수행
if dfs(i,j) == True:
result += 1
print(result)
✔️나의 문제풀이와 책의 문제풀이 비교 및 느낀점
- 입력조건은 만족
- 재귀를 좌표로 이용하기
- 느낀점
- 격자가 주어지면 범위 벗어나지 않도록 규제하기(if x <= -1 or x >= n or y <= -1 or y >= m)
- bool로 조건 규제하기
📌4. 미로 탈출
✔️문제
N * M 크기의 직사각형 형태의 미로. 미로에는 여러 마리의 괴물이 있어 피해서 탈출해야한다.
현재 위치는 (1,1), 미로의 출구는 (N,M)의 위치에 존재하며 한 번에 한 칸씩 이동할 수 있다.
괴물이 있는 부분은 0, 괴물이 없는 부분은 1로 표시.(미로는 탈출할 수 있는 형태로 제시된다.)
사람이 탈출하기 위해 움직여야하는 최소 칸의 개수는?
✔️입력조건
- 첫째 줄에 두 정수 N,M(4 <= N,M <= 200)이 주어진다.
- 다음 N개의 줄에는 각각M개의 정수(0,1)로 미로의 정보가 주어진다.
각각의 수들은 공백 없이 붙어서 입력으로 제시된다. 또한 시작 칸과 마지막 칸은 항상 1이다.
✔️출력 조건
첫째 줄에 최소 이동 칸의 개수를 출력한다.
✔️입력 예시
5 6
101010
111111
000001
111111
111111
✔️출력 예시
10
✔️나의 문제 풀이
- 인접 큐 조건 해결하지 못함
from collections import deque
n,m = map(int,input().split())
cnt = 0
graph = []
for _ in range(n):
graph.append(list(map(int, input()))) # 2차원 리스트 만들때 append 안에 list!!!!
# BFS(연결되어 있음)
def bfs(x,y):
global cnt
if x <= 0 or x > n or y <= 0 or y > n:
return False
if graph[x][y] == 1:
queue = deque()
queue.append(graph[x][y])
cnt += 1
while queue:
queue.popleft()
graph[x][y] = 0
for i in range(x,n+1):
for j in range(y, m+1):
if graph[i][j] == 1:
if graph[i-1][j] == 1 or graph[i+1][j] == 1 or graph[i][j-1] == 1 or graph[i][j+1] == 1:
# 인접 큐인거 조건 걸어주기
queue.append(graph[i][j])
cnt += 1
return True
print(queue)
return False
bfs(1,1)
print(cnt)- (0,1), (1,0)만 고민, deque사용하지 않음
n,m = map(int,input().split())
graph = []
ans = 1
for _ in range(n):
graph.append(list(map(int,input())))
def bfs(x,y):
if y+1 < m and graph[x][y+1] == 1:
x,y = x, y+1
elif x+1 < n and graph[x+1][y] == 1:
x,y = x+1,y
return x,y
x,y = 0,0
while x < n and y < m:
if graph[x][y] == 1:
x,y = bfs(x,y)
ans += 1
if x == n-1 and y == m-1:
break
print(ans)✔️책의 문제 풀이
- BFS를 이용. 시작 지점에서 가까운 노드부터 차례대로 스래프의 모든 노드 탐색
- 모든 노드의 값을 거리 정보로 넣기(특정 노드 방문 시, 이전 노드 거리 + 1)
- 첫번째 시작 위치는 다시 방문할 수 있도록하여 시작 위치 값이 3으로 변경될 수 있음
- 시작 위치의 값이 1이 아닌 3으로 바뀐 상태여서 탐색하지 않음(1인 것만 탐색)
from collections import deque
# N,M을 공백으로 구분하여 입력받기
n,m = map(int,input().split())
# 2차원 리스트의 맵 정보 입력받기
graph = []
for i in range(n):
graph.append(list(map(int, input())))
# 이동할 네 방향 정의(상, 하, 좌, 우)
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
# BFS 소스코드 구현
def bfs(x,y):
# 큐 구현을 위해 deque 라이브러리 사용
queue = deque()
queue.append((x,y))
# 큐가 빌 때까지 반복
while queue:
x, y = queue.popleft()
# 현재 위치에서 네 방향으로의 위치 확인
for i in range(4):
nx = x + dx[i]
ny = y +dy[i]
# 미로 찾기 공간을 벗어난 경우 무시
if nx < 0 or ny < 0 or nx >= n or ny >= m:
continue
# 벽인 경우 무시
if graph[nx][ny] == 0:
continue
# 해당 노드를 처음 방문하는 경우에만 최단 거리 기록
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1 # 노드의 값을 거리 정보로 넣기
queue.append((nx, ny))
# 가장 오른쪽 아래까지의 최단 거리 반환
return graph[n - 1][m - 1]
# BFS를 수행한 결과 출력
print(bfs(0,0))
✔️나의 문제풀이와 책의 문제풀이 비교 및 느낀점
- deque 이용하는 기본틀은 동일, 조건만 신경써서 작성하기
- 이동 뱡향 정의 생각하기!!
- 노드 값을 거리 정보로 넣는거 생각하기(좌표 값이랑은 또 다른값, 이걸 사용하면서 cnt를 정의하지 않아도 됨)
'Coding Test > 이것이 취업을 위한 코딩테스트이다 with 파이썬' 카테고리의 다른 글
| [이것이 취업을 위한 코딩테스트이다 with 파이썬] Ch.12 구현 문제 (0) | 2023.03.22 |
|---|---|
| [이것이 취업을 위한 코딩테스트이다 with 파이썬] Ch.15 이진 탐색 문제 (0) | 2023.03.17 |
| [이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.11 그리디 문제 (0) | 2023.03.06 |
| [이것이 취업을 위한 코딩테스트이다 with 파이썬] Ch.14 정렬 문제 (0) | 2023.03.02 |
| [이것이 취업을 위한 코딩테스트다 with 파이썬] Ch.9 최단 경로 (0) | 2022.04.29 |




